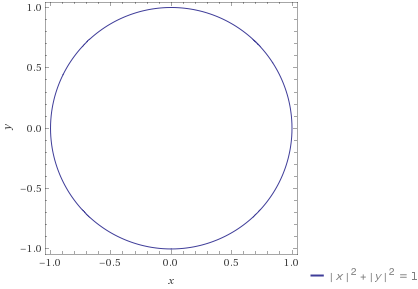
Please notice that the above is an "equation" in Cartesion coordinates, not a "function". There are various functional forms for the circle, such as in polar coordinates, but for the purposes of this post we'll stick with the above equation.
There are four "easy" points for this equation, which occur when each term of the equation is set to zero, in which case the other term is forced to take on values of +1 and -1 (the two real values whose squares equal positive one). These four points are called the "zeros" and occur at the following coordinates:
Here's a plot of the above equation (courtesy of WolframAlpha):
As expected, we have a circle with radius 1. Take a moment to verify that each of the zeros is indeed present.
Next, let's look at the "generalized" form of this equation, where the common exponent can take on other values:
This represents the family of equations where the exponent of x and y is the same. However, this form has some specific limitations we need to address before we start to play with values for n other than 2.
First, we need to constrain the equation to generate non-negative values so the sum is both real and bounded. For example, if n were odd, such as 3, then negative values of x and y would take on negative values when cubed, which in turn would force the other term to take on larger positive values to obtain the sum of positive 1, yielding a poorly-constrained result.
We will constrain the equation in three ways:
- Apply the exponent to the absolute value of x and y, instead of the value itself. This will ensure the resulting exponentiation will always yield a positive value.
- Explicitly limit the values of x and y to be in the range of positive and negative 1.
- Limit n to be strictly greater than zero. Please explore for yourself why this is important, though it may be best to wait to do so until after reaching the end of this post.
Here's the full form of our generalized, but constrained, equation:
To be sure we haven't created a monster, let's look at the plot of this equation for the case n = 2:
Good! It's still a circle with radius 1.
Notice that the point (0,0) is still at the center, but for this plot I have chosen not to draw the conventional Cartesian axes through (0,0), but I instead used axis labels and legends at the sides of the plot. This was done not only to keep the plot itself as uncluttered as possible (which will become important later), but also to better depict the explicit bounds on x and y. Everything we do going forward will literally be "inside the box".
Ready to play?
Let's start with a look at the plot after setting n = 1:
Whoa, a diamond? It makes sense when you think about it: This is a linear equation, so these are the four line segments connecting the zero points.
But how did the circle of n = 2 become the diamond of n = 1? Let's look at the plot for a value of n between 2 and 1, say n = 1.5:
What's this? A "puffy diamond" or a "squeezed circle"? Notice that we obtained a plot for a value of n between 1 and 2 that has a mix of the characteristics for the plots of n = 1 and n = 2. This is not at all guaranteed, and the plots of many generalized equations fail to have this property as clearly evident as it is for this specific simple equation.
OK. So plots for values of n between 1 and 2 also "fall between" the plots for n = 1 and n = 2. What should we expect the plots for values of n < 1 to look like? Let's try n = 0.5:
Cool! A star! Notice that our four zeros are still there. Also notice that as n has decreased from 2, the "corners" along the diagonals have steadily moved in. Another way to look at this is to view the portions of the plot near the zeros as getting "pointier" as n decreased.
Take a closer look at the legend accompanying the above plot: The exponent of 1/2 has been replaced with a square root radical. This should be a hint for describing the curve in each quadrant. Can you say what curve it is?
Let's look at the plot for a lower value, for n = 0.25:
Yup, an even pointier star. Perhaps one with a twinkle? It follows our intuition that the plot should get "pointier" at the zeros as the value of n decreases.
What about the plots for n > 2? What does our intuition tell us? A n increases, we should expect the plot at the zeros to get rounder, and the plot diagonals to move further outward. Let's take a look for n = 3:
What's this? A "square-ish circle" or "circle-ish square"? Actually, the set of plots for all n > 2 has it's own name: They're called "squircles".
Let's double n, and see what happens for n = 6. What do you think it will look like?
Yup, it's getting more square. Notice that the sides aren't completely flat: They are still ever-so-slightly rounded. But it doesn't look quite like the "rounded squares" we may be used to, where the corners are simply rounded to a circular arc.
Are squircles of any use? In iOS 7, Apple switched their icon outline from a rounded rectangle to a squircle with n = 5:
Not much of a difference from n = 6, but how about compared to a rounded rectangle?
Ah, see the difference? Which icon shape do you find to be most pleasing? Personally, I find the squircle more elegant, making the rounded square look to have corners at each end of each corner's arc.
Why did Apple make the change? Well, Apple may have wanted to make the change earlier, but it wasn't until iOS7 that most iPhones had screens with high enough resolution to make the difference visible enough to appreciate.
Finally, here's a plot combining the plots for n = {0.25, 0.5, 1, 1.5, 2, 3, 5}, making it more clear how the curves change with n and how the zeros are preserved: